Expect the Uexpected

15/12/21 17:30 Filed in: Software Engineering
There are certain classes in science and mathematics that computer science and software engineering people don't think they will need in a real job. These include:
  • finite arithmetic,
  • the limits of measurement; and,
  • quantum physics.
Unfortunately if you work with real numbers, measure anything or interact with time your simple straight forward problem turns into a twisty mess of complex cases as you do your best with what information you have.

We frequently drop complexity out by making useful models of the world. This simplification allows us to make a solution. But the next step is add back in the relevant bits where the real world upsets our model.

Be on the look out for places where those difficult cases might turn up and not let them arrive unexpected.

Finite Arithmetic



If you use a float or double in nay part of your program then the number is not exact. Most of the time, you won't notice this. But you can run out of mantissa:

#!/usr/bin/env python
A=10000000000000005.0
B=10000000000000003.0

print((A-B))


Produces 0.0 not what you would expect (2.0).

Subtracting numbers with small differences and multiplying by large numbers:

!/usr/bin/env python
A=1.000002
B=1.000001
C=0.000001
D=1e20

print(((A-B)-C)*D)


Produces 13977.8012231 not what you would expect (0.0)

And while these are examples are contrived you can see this in real world situations. I chose to represent a distance in meters instead of kilometres and had to work very hard to get a result to the required precision in the units required.

Limits of Measurement



Nyquist's theorem paraphrased says that you need to sample at at least twice the rate of the highest frequency you want to capture.

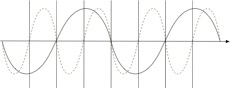
sample

At the sample rate shown the solid black line's frequency can estimated, the green dotted line cannot be estimated.

This shows up in all sorts of places from share trading to counting the number of times a contact closes.

Observation



Heisenberg's Uncertainty Principal seems pretty exotic (if you know the location of a particle to a particular accuracy, you can only know its location to a particular accuracy and the better you know its location the less well you know its speed) but we get observer effects in computers too.

Adding debugging consumes resources (even measuring a signal with an oscilloscope affects it) so the act of measuring affects the measurement. Heisenbugs ie bugs that depend on precise timing (frequently between threads) disappear when you turn on the debugging.

Time is a particularly squirrelly issue:
  • "Man with two watches never knows the time" might be from a fortune cookie, but its actually true
  • When you synchronise time, what happens if it moves backwards (yes you can adjust the clock rate but you are wrong while you are), can your program cope with time moving backwards?
  • You can sample time but this takes time so you actually only know it to within an error bound

And these pop up in real time systems

Conclusion



The real world is not a simple place and pretending it isn't (its called making a model) is a really useful start, but then you need to add back in handling for the ugly bits you simplified out or the unexpected will win.

Tags: